良心周赛 四题代码总共不超过50行🥺
第一题:分割字符串的最大得分
难度简单
题目描述
给你一个由若干 0 和 1 组成的字符串 s ,请你计算并返回将该字符串分割成两个 非空 子字符串(即 左 子字符串和 右 子字符串)所能获得的最大得分。
「分割字符串的得分」为 左 子字符串中 0 的数量加上 右 子字符串中 1 的数量。
示例 1:
|
1 2 3 4 5 6 7 8 9 10 |
输入:s = "011101" 输出:5 解释: 将字符串 s 划分为两个非空子字符串的可行方案有: 左子字符串 = "0" 且 右子字符串 = "11101",得分 = 1 + 4 = 5 左子字符串 = "01" 且 右子字符串 = "1101",得分 = 1 + 3 = 4 左子字符串 = "011" 且 右子字符串 = "101",得分 = 1 + 2 = 3 左子字符串 = "0111" 且 右子字符串 = "01",得分 = 1 + 1 = 2 左子字符串 = "01110" 且 右子字符串 = "1",得分 = 2 + 1 = 3 |
示例 2:
|
1 2 3 4 |
输入:s = "00111" 输出:5 解释:当 左子字符串 = "00" 且 右子字符串 = "111" 时,我们得到最大得分 = 2 + 3 = 5 |
示例 3:
|
1 2 3 |
输入:s = "1111" 输出:3 |
提示:
2 <= s.length <= 500- 字符串
s仅由字符'0'和'1'组成。
题目链接
https://leetcode-cn.com/problems/maximum-score-after-splitting-a-string/
思路:
遍历每一个分割位置。
代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
class Solution: def maxScore(self, s: str) -> int: n = len(s) ans = 0 for i in range(1, n): left = s[:i] right = s[i:n] score = left.count('0') + right.count('1') ans = max(ans, score) return ans |
第二题:可获得的最大点数
难度中等
题目描述
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。
每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。
你的点数就是你拿到手中的所有卡牌的点数之和。
给你一个整数数组 cardPoints 和整数 k,请你返回可以获得的最大点数。
示例 1:
|
1 2 3 4 |
输入:cardPoints = [1,2,3,4,5,6,1], k = 3 输出:12 解释:第一次行动,不管拿哪张牌,你的点数总是 1 。但是,先拿最右边的卡牌将会最大化你的可获得点数。最优策略是拿右边的三张牌,最终点数为 1 + 6 + 5 = 12 。 |
示例 2:
|
1 2 3 4 |
输入:cardPoints = [2,2,2], k = 2 输出:4 解释:无论你拿起哪两张卡牌,可获得的点数总是 4 。 |
示例 3:
|
1 2 3 4 |
输入:cardPoints = [9,7,7,9,7,7,9], k = 7 输出:55 解释:你必须拿起所有卡牌,可以获得的点数为所有卡牌的点数之和。 |
示例 4:
|
1 2 3 4 |
输入:cardPoints = [1,1000,1], k = 1 输出:1 解释:你无法拿到中间那张卡牌,所以可以获得的最大点数为 1 。 |
示例 5:
|
1 2 3 |
输入:cardPoints = [1,79,80,1,1,1,200,1], k = 3 输出:202 |
提示:
1 <= cardPoints.length <= 10^51 <= cardPoints[i] <= 10^41 <= k <= cardPoints.length
题目链接
https://leetcode-cn.com/problems/maximum-points-you-can-obtain-from-cards/
思路:
因为拿掉的牌固定为k张,因此剩下的就是中间的n-k张,维护一个滑动窗口,求中间n-k张的最小值即可。
代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
class Solution: def maxScore(self, cardPoints: List[int], k: int) -> int: n = len(cardPoints) - k if n == 0: return sum(cardPoints) left = 0 wnd = 0 ans = inf for right, num in enumerate(cardPoints): # cardPoints[left: right+1] wnd += num if right + 1 - left == n: # 窗口内的数量正好为n ans = min(ans, wnd) wnd -= cardPoints[left] # 减掉一个 left += 1 return sum(cardPoints) - ans |
第三题:对角线遍历 II
难度中等
题目描述
给你一个列表 nums ,里面每一个元素都是一个整数列表。请你依照下面各图的规则,按顺序返回 nums 中对角线上的整数。
示例 1:
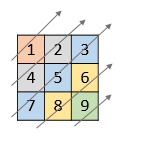
|
1 2 3 |
输入:nums = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,4,2,7,5,3,8,6,9] |
示例 2:
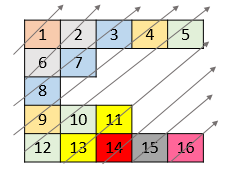
|
1 2 3 |
输入:nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]] 输出:[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16] |
示例 3:
|
1 2 3 |
输入:nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]] 输出:[1,4,2,5,3,8,6,9,7,10,11] |
示例 4:
|
1 2 3 |
输入:nums = [[1,2,3,4,5,6]] 输出:[1,2,3,4,5,6] |
提示:
1 <= nums.length <= 10^51 <= nums[i].length <= 10^51 <= nums[i][j] <= 10^9nums中最多有10^5个数字。
题目链接
https://leetcode-cn.com/problems/diagonal-traverse-ii/
思路:
在同一条对角线上的元素,横纵坐标之和是相等的,也就是i+j是一样的。
计算所有元素的横纵坐标,然后按照(横纵坐标之和,纵坐标,元素值)的关键字顺序来排序,排序后的结果就是对角线遍历的顺序。
代码:
|
1 2 3 4 5 6 7 8 9 10 11 |
class Solution: def findDiagonalOrder(self, nums: List[List[int]]) -> List[int]: ans = [] for i, line in enumerate(nums): for j, num in enumerate(line): ans.append((i+j,j,num)) ans.sort() return [x[2] for x in ans] |
第四题:带限制的子序列和
难度困难
题目描述
给你一个整数数组 nums 和一个整数 k ,请你返回 非空 子序列元素和的最大值,子序列需要满足:子序列中每两个 相邻 的整数 nums[i] 和 nums[j] ,它们在原数组中的下标 i 和 j 满足 i < j 且 j - i <= k 。
数组的子序列定义为:将数组中的若干个数字删除(可以删除 0 个数字),剩下的数字按照原本的顺序排布。
示例 1:
|
1 2 3 4 |
输入:nums = [10,2,-10,5,20], k = 2 输出:37 解释:子序列为 [10, 2, 5, 20] 。 |
示例 2:
|
1 2 3 4 |
输入:nums = [-1,-2,-3], k = 1 输出:-1 解释:子序列必须是非空的,所以我们选择最大的数字。 |
示例 3:
|
1 2 3 4 |
输入:nums = [10,-2,-10,-5,20], k = 2 输出:23 解释:子序列为 [10, -2, -5, 20] 。 |
提示:
1 <= k <= nums.length <= 10^5-10^4 <= nums[i] <= 10^4
题目链接
https://leetcode-cn.com/problems/constrained-subset-sum/
思路:
动态规划。令dp[i]表示选择下标为i的元素时能选择的最大子序和,因为选择的两个元素下标之差不能大于k,因此有状态转移方程dp[i] = max(0, max(dp[i-k: i])) + nums[i]。
由于题目的范围较大,不能暴力计算max(dp[i-k: i]),因此使用一个最大堆来保存dp[i-k: i]的最大值。
代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
class Solution: def constrainedSubsetSum(self, nums: List[int], k: int) -> int: n = len(nums) dp = [0] * n heap = [] ans = nums[0] for i in range(n): num = nums[i] dp_j = float('inf') while heap: dp_j, j = heapq.heappop(heap) if j >= i - k: heapq.heappush(heap, (dp_j, j)) # 放回去 break dp[i] = max(0, -dp_j) + num print(i, dp[i]) if dp[i] > 0: heapq.heappush(heap, (-dp[i], i)) ans = max(ans, dp[i]) return(ans) |
